Прежде, чем рассматривать выполнение машинных программ аппаратурой ЭВМ, рассмотрим представление в памяти машины чисел, а также алфавитно-цифровых символов. Это представление потребуется нам в дальнейшем при изучении машинных программ, а также обрабатываемых ими данных.

1.1 Двоичные числа

Чтобы сделать вычислительные системы более надежными и простыми, их аппаратура строится из простейших электронных схем, которые могут находиться только в двух состояниях. Одно из них обозначается 0, а другое – 1. Такая схема предназначена для длительного или краткого хранения самой мелкой единицы информации – бита  (от «BInary  digiT» – двоичная цифра).

Любое число можно представить в виде цепочки битов. Такое представление числа называется двоичным числом. Цепочка из восьми битов называется байтом (рис. 1).

10011011

старший бит (бит 7)          младший бит (бит 0)

Рис. 1. Пример байта

   Величина двоичного числа определяется относительной позицией каждого бита и его значением. Позиционный вес младшего бита 2^о = 1(10), где 1(10) – единица в десятичной системе счисления. Следующий бит имеет вес 2¹ = 2(10). Вес любой позиции получается удвоением веса предыдущей позиции (рис. 2).

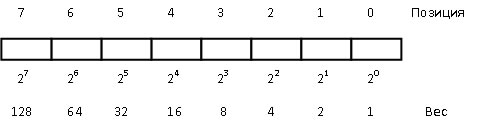
Рис. 2. Веса позиций байта

Для преобразования десятичного числа в двоичное можно использовать один из двух методов – метод деления и метод вычитания. Первый из этих методов широко используется в программах, выполняющих преобразование чисел из одной системы счисления в другую. Этот метод будет рассмотрен нами в других разделах, при описании соответствующих программ. Сейчас мы будем использовать метод вычитания, главное достоинство которого – наглядность. Согласно этому методу, для преобразования десятичного числа в двоичное надо сделать ряд вычитаний, каждое из которых даст значение  одного бита.

Прежде всего, вычтите из десятичного числа наибольший возможный двоичный вес и запишите 1 в эту позицию бита. Затем из результата вычтите новый наибольший возможный двоичный вес и запишите 1 в эту новую позицию бита. Так - до получения нулевого результата. Например, преобразование числа 50 в двоичное:

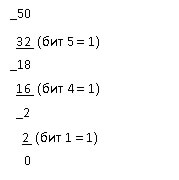
Записывая 0 в остальные позиции битов (биты 0,2,3) получаем окончательный результат:  110010.

Для выполнения обратного преобразования следует сложить десятичные веса тех позиций, в которых стоит 1:

32 (бит 5) + 16 (бит 4) + 2 (бит 1) = 50

Байт может представлять десятичные положительные числа от 0 (00000000) до 255 (11111111). Число 255 может быть получено двумя способами: 1) суммированием весов всех битов байта; 2) по формуле 2⁸ – 1, где 8 – номер первого бита, не вошедшего в состав байта.

Оперативная память ЭВМ состоит из блоков памяти по 1024 байта. Число 1024 есть 2¹⁰. Число 1024 имеет стандартное обозначение К. Следовательно, ЭВМ, имеющая 48 К памяти, содержит 48 x 1024 = 49152 байта.

Машинным словом будем называть битовую строку длиной 16 битов. Одно слово  содержит 2 байта (рис. 3). Каждый бит слова имеет свой вес. Просуммировав все веса, найдем максимальное целое число без знака, которое можно записать в одно слово, оно равно  2¹⁶ – 1 = 65535.

Двоичное содержимое байта или слова может рассматриваться (интерпретироваться) как число без знака и как число со знаком. Число без знака занимает все 16 битов слова или 8 битов байта. Оно может быть только положительным. Просуммируем два таких числа:

    00111100                                   60 (10)

+  10110101                               +181 (10)

    11110001                                 241 (10)

Обратим внимание, что единица, появившаяся в старшем бите результата, свидетельствует лишь о возросшей величине результата, который для беззнаковых чисел может быть только неотрицательным.

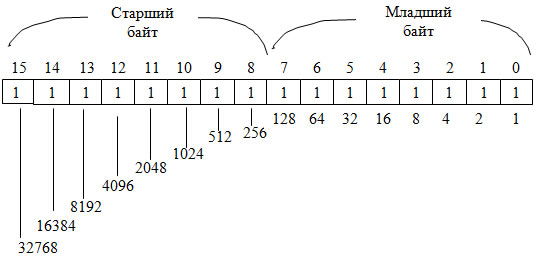
Рис. 3. Веса позиций слова

Если слово (байт) содержит число со знаком, то в старшем бите содержится знак  (0 есть +, 1 есть -), а оставшиеся 15 или 7 битов содержат само число в дополнительном коде. Дополнительный код положительного числа совпадает с записью такого же числа без знака. Для получения дополнительного кода отрицательного числа из его абсолютного значения используется следующее правило:

все биты числа (в том числе и знаковый) инвертируются;

к полученному числу прибавляется 1.

Например, получим дополнительный код числа –65:

                       65(10) = 01000001(2)

   1)                             10111110

   2)                         +               1

                                    10111111 = -65(10)

Для получения абсолютного значения отрицательного числа повторяют эти же самые  два действия. Например:

                       -65(10)= 10111111

                       1)         01000000

                       2)       +            1 

                                    01000001 = 65(10)

Сумма +65 и –65 должна составить ноль:

                                  01000001  (+65)

                               + 10111111  (-65)

                                  00000000

В данном примере у нас произошли два интересных переноса: 1) в знаковый (7-й) разряд; 2) за пределы байта. Первая единица переноса обрабатывается как обычно, а вторая теряется. Оба переноса считаются правильными.

Вычитание двух положительных чисел заменяется суммированием первого числа с дополнением второго. Таким образом, как суммирование, так и вычитание выполняет одно и то же аппаратное устройство – сумматор. Кроме этого свойства использование дополнения имеет еще одно достоинство - число  ноль  имеет единственное представление, т.е. нет двух нулей – положительного и отрицательного. Приведем целые числа в окрестностях 0:

+ 3   00000011

+ 2   00000010

+ 1   00000001

   0   00000000

    -  1   11111111

    -  2   11111110

    -  3   11111101

Отсюда видно, что нулевые биты в отрицательном двоичном числе фактически определяют его величину: рассмотрите весовые значения нулевых битов так, как если бы это были единичные биты, сложите эти значения и прибавьте 1.